Since originally posting this I realized the dynamometer data I was using measured the torque being produced at the wheel not at the engine crankshaft. Consequently, my reducing the “engine torque” to reflect drive train losses was incorrect (I was double-counting the effective losses). I’ve updated the files and charts to reflect the correction.

---

The other day on a ride down to Santa Cruz I found myself behind a sequence of what I call Grandpa Go Slow vehicles. Don’t get me wrong: it was great to see so many people finally enjoying our beautiful California coast. It’s just that, while I don’t ride fast¹ I do like to go the speed limit². With all the vehicles out there the passing opportunities were relatively small. So I was incentivized to figure out how to pass cars quickly.

Turns out I hadn’t been using the bike’s engine properly heretofore. I was doing what I used to do in manual transmission cars, dropping down one gear to increase the power to the wheels. Only motorcycle engines are designed to run at much higher RPMs than most car engines…and, roughly speaking, power equals RPM times torque. The faster you run the engine — which happens when you downshift — the more power you have to accelerate…and a bike engine will happily turn at rates which would cause your typical car engine to seize up.

When I got home I thought it’d be fun to explore the mathematics and physics of this. I loved the introduction to mathematical physics course I took in college and was quite good at solving the oddball problems such textbooks always include³.

But, uhh, it turns out I’ve forgotten a lot of physics in the almost 50 years since I took that course. I spent over an hour struggling with converting the engine’s torque to linear acceleration before I remembered that torque is “force at a distance”, so to get the force caused by a torque you have to divide torque by the radius of the wheel it’s turning. This despite the fact the numbers I was using for torque were helpfully labeled “newton-meters” and I knew that a newton is a unit of force. My prof who taught me the importance of dimensional analysis⁴ would have flunked me. Oh well.

In the end I came up with a neat little Excel spreadsheet which you can download from here. It walks you through how the torques, speeds and accelerations are calculated. It also contains some interesting charts.

Here’s the torque produced by a Yamaha FJR-1300 engine:

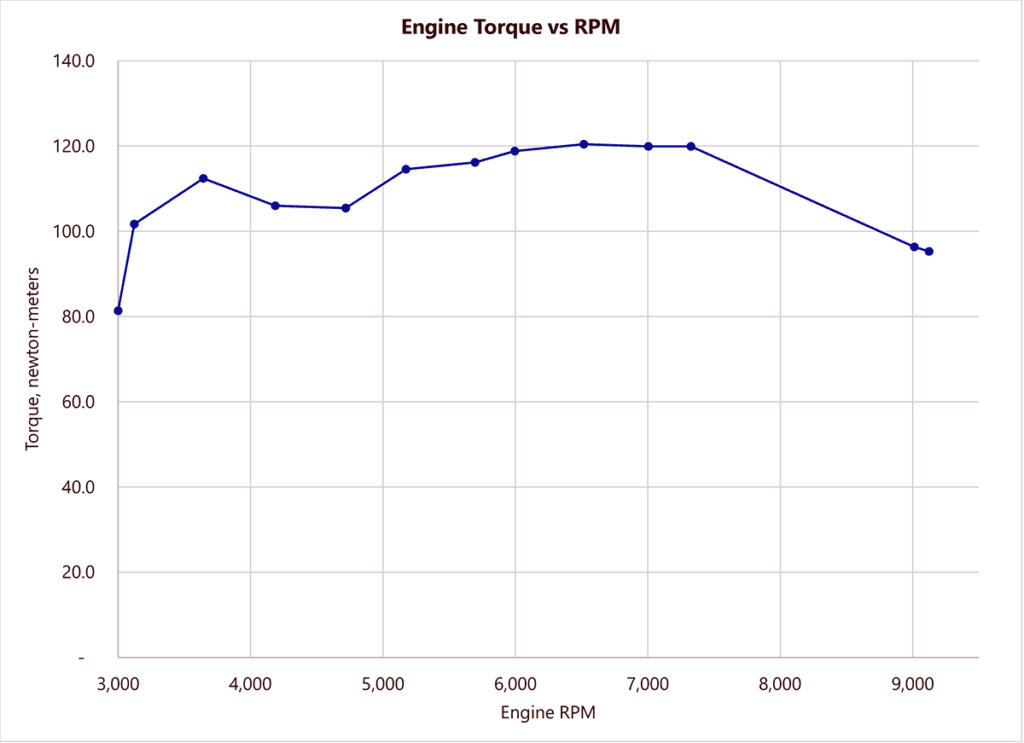
The pretty flat curve is a good thing. It means the power the engine will apply to the rear wheel is pretty much a direct function of how fast the engine is turning over (i.e., its RPM).

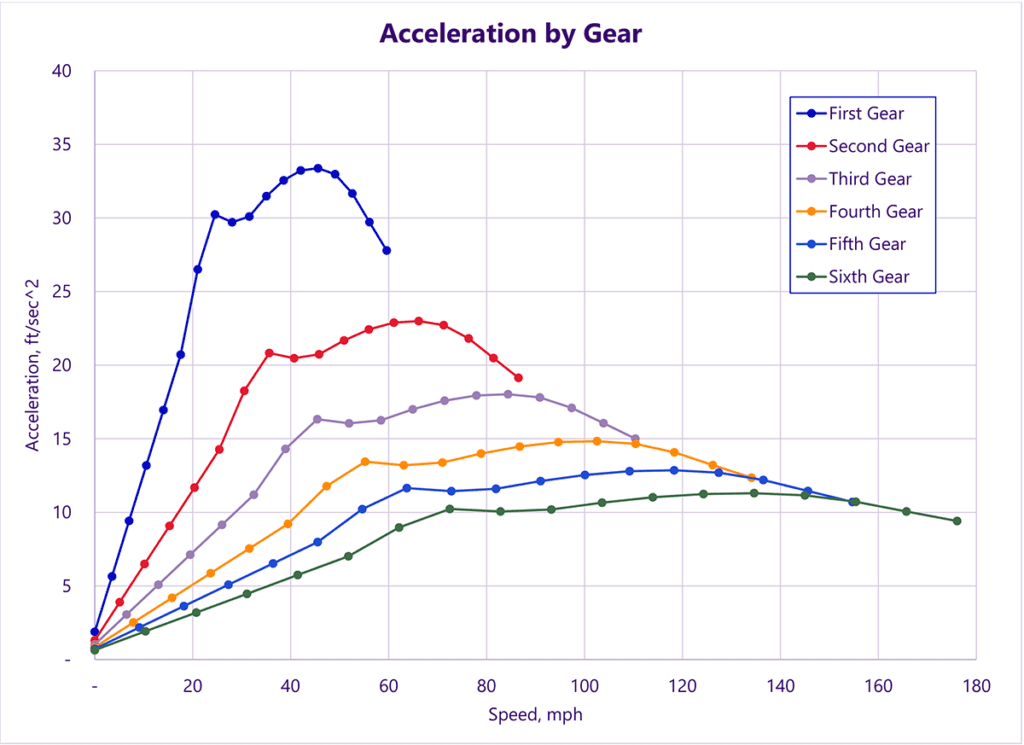
Here are the acceleration curves for each gear on the bike, plotted against the speed the bike is moving. Remember that 1 gee — the force of gravity at the Earth’s surface — is 32 feet per second squared. Pulling one gee of acceleration in first gear (roughly the maximum) may not be as good as a rocket or a jet but it ain’t hay, neither. Which explains why you have to hold on tight to a bike when you push it.

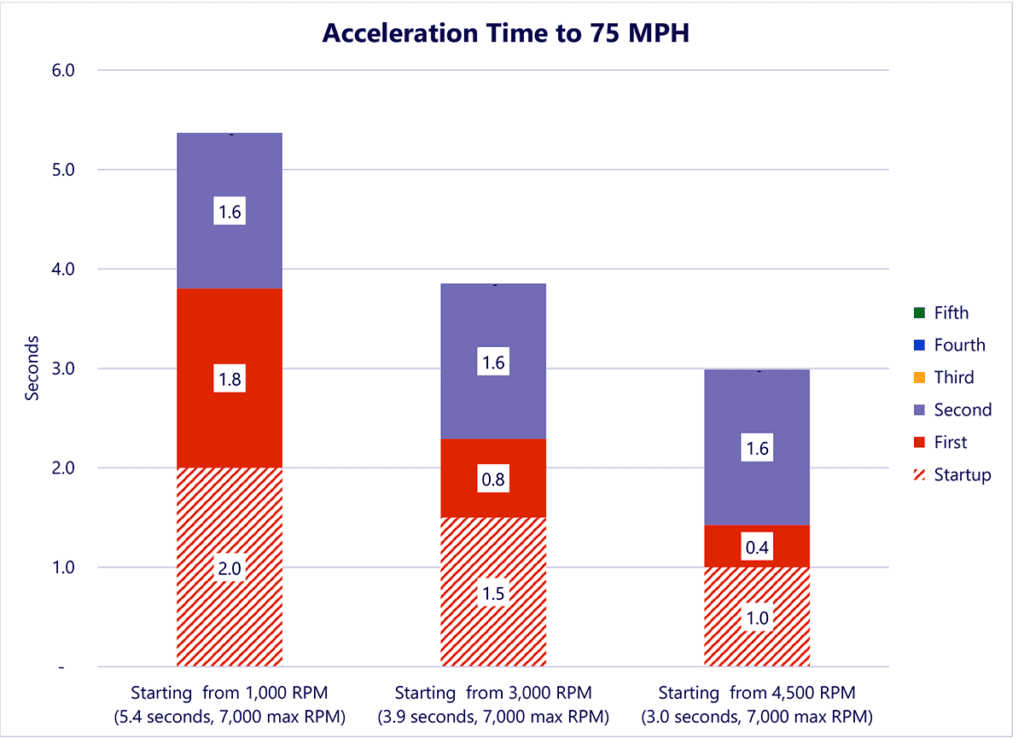
Finally, here’s a chart showing some alternative trajectories getting to 75 mph. The Startup stage is when you’re taking off from a stop but have revved the engine (to the indicated RPM level) and are releasing the clutch to engage first gear. FYI, the FJR-1300 idles at 1,000 RPM so that alternative is basically taking off from idle and then twisting the throttle hard.

Enjoy!

---

Here’s the entire Excel file as a PDF:

FJR-1300-Acceleration

---

1. at least compared to other riders ↩

2. or maybe a bit over ↩

3. I remember one involving calculating the trajectory and time to drop of a marble let loose into the top of a spinning hollow cone. That was a bit of a mind-bender! ↩

4. paying attention to the dimensions that the numbers are reporting ↩