A Surprising Story of Space, Time and Mathematical Transformation,
by Robyn Arianrhod
University of Chicago Press
Science fiction readers are familiar with being confronted with real scientific or mathematical terms they don’t know. For me, one of those terms was tensor. Which is a mathematical entity or structure that I never encountered in my math classes.
It crops up all the time in any discussion of Einstein and his theory of general relativity, in which tensors figure prominently. I even own a tee shirt sporting the Einstein field equation:
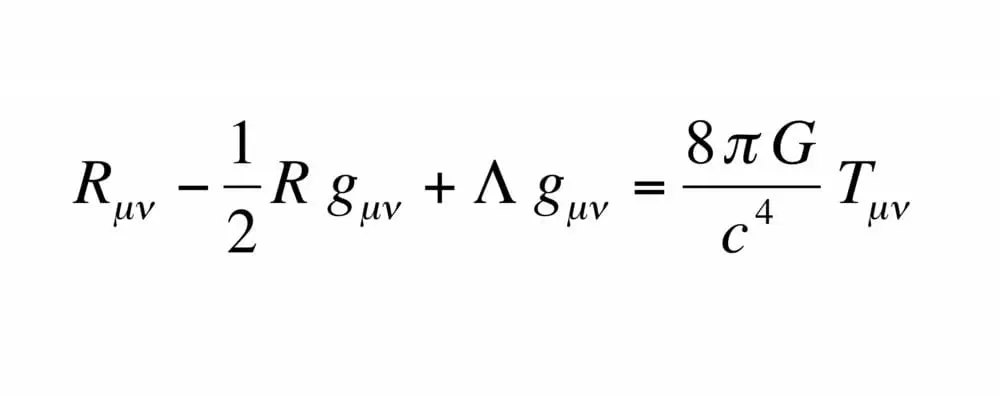
Those R, g and T things sporting the mu and nu lower-case Greek letters are tensors.

Needless to say, that tee shirt gets a lot of attention at the college gym I work out at. But apparently no physics majors work out when I do, because no one has correctly identified it :).
I had a vague sense throughout my life that tensors were some kind of generalization of vectors. But it was all pretty hazy. So, you can imagine my excitement when I read a review of Robyn Arianrhod’s book Vectors, in which it was noted she explains what tensors are and why they’re important. At last! I could cross another item off my bucket list!
What really impressed me about Arianrhod’s book, though, was not the part about tensors (although that was really cool), but how mathematics evolved over millennia (from its origin as an aid in wealth and income accounting) through geometry, algebra and calculus to where we are today (which is by no means the culmination).
Even more fascinating was her showing how mathematics evolved, as one generation after another built on their predecessors’ work, in large part by recognizing patterns that occurred while using the earlier work that hinted at more profound generalizations. Put another way, Arianrhod humanized one of the most abstract endeavors the human race has ever pursued. And which has given us more cool gadgets, tools and toys than any of our ancestors could have dreamed of.
In fairness, about a third of the book hovered at the edge of my comprehension. But that wasn’t a fault of Arianrhod’s style or exposition! It’s just that I only studied math through elementary calculus, differential equations and linear algebra…a long time ago. Little did I know how much exciting and powerful stuff lurked past the place where I stopped.
Reading Vector makes me want to return to those studies from decades ago and restart them. Because even when I was only dimly grasping what Arianrhod was saying, I could sense the power and beauty of very powerful mathematics.
Geometry and Algebra
Don’t get me wrong, I got a lot out of the book (and I plan on re-reading it, going through the copious end note explanations and proofs she includes)! For one thing, she tied together some geometric and algebraic concepts that I’d always been curious about.
Remember “imaginary” numbers? Like the square root of any negative number? The very name implies there’s something not quite right about them, that they aren’t “real”.
But they are. The reason they seem odd to us is because our definition of “number”, while grounded in the real world, is too limited. There is a dimensionality inherent in any number that we can generally ignore in day-to-day use. Put another way, the number 4 is better represented by (4, 0), with the second component having no value (which is why it can be ignored in ordinary use). The square roots of (4, 0) are (2, 0) and (-2, 0), where again you can ignore that second component.
But the square roots of (-4, 0)? Those are (0, 2) and (0, -2); the second component is, even though it’s dubbed “imaginary”, now essential. You can’t define the square root of a negative number without that second component1.
It turns out there’s a really interesting relationship between two-dimensional numeric values (“complex numbers”, things with a “real” and “imaginary” part) and geometry. What’s even more interesting, as Arianrhod wonderfully explains, is the relationship is a hint of a very deep connection between geometry and algebra.
In fact, it seems like the major discovery in mathematics in the 19th century was the recognition and exploration of that deep connection. Along the way it gave rise to the realization that what most of us think of as algebra is only one of a number of algebras, some with rules which are critical to representing reality mathematically, but which don’t “obey” standard algebraic rules.
Vectors is worth reading just to get a sense of how marvelous and important this exploration and its results are.
Changing Perspectives Can Lead to Insights
But back to the “entry level” linkage I mentioned above. When numeric values have multiple dimensional components, it’s natural to think about graphing them2. While most of us would do so by immediately reaching for traditional graph paper, it’s important to remember two-dimensional numeric values can be represented by not just by their X and Y coordinates, but by an angle and a radius as well.
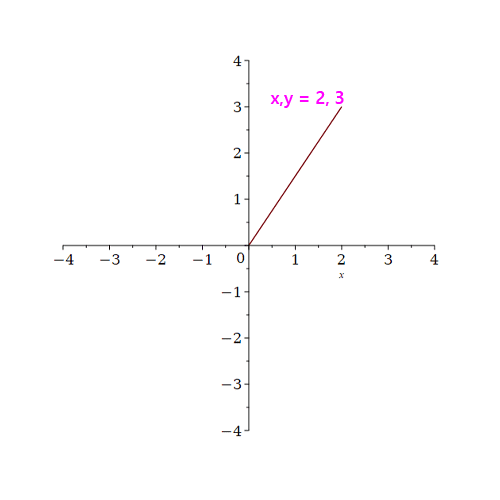
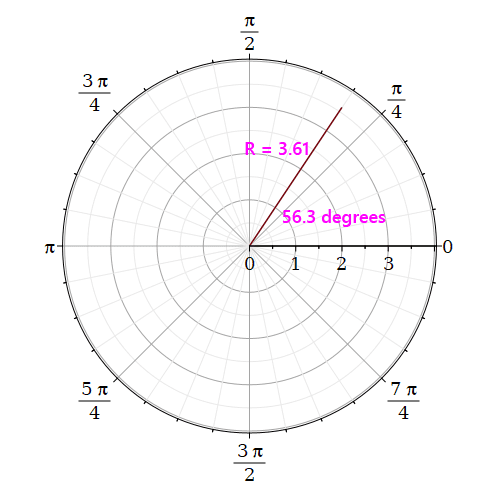
That may not seem important, but it is, due to one of the most famous equations in all of mathematics, the Euler relation:
R {\mathrm e}^{\mathrm{I} \theta}=R \cos\! \left(\theta \right)+\mathrm{I} R \sin\! \left(\theta \right)What this says is that any complex (two-dimensional) value can be represented as a real number (R) and an angle (θ) (I is the unitary “imaginary” number).
Importantly, because trigonometric functions are cyclical — they repeat every 360 degrees or two π radians — you could expand that relationship like this:
R {\mathrm e}^{\mathrm{I} \left(2 \pi k+\theta \right)}=R \cos\! \left(2 \pi k+\theta \right)+\mathrm{I} R \sin\! \left(2 \pi k+\theta \right)where k can take on any integer value starting from 0: 0, 1, 2, 3… Which, when you take the nth order root of a two-dimensional value becomes:
R^{\frac{1}{n}} {\mathrm e}^{\frac{\mathrm{I} \left(2 \pi k+\theta \right)}{n}}=R^{\frac{1}{n}} \cos\! \left(\frac{\theta}{n}+\frac{2 \pi k}{n}\right)+\mathrm{I} R^{\frac{1}{n}} \sin\! \left(\frac{\theta}{n}+\frac{2 \pi k}{n}\right)Which highlights an important relationship between numeric values and their roots. Just like there are two equally valid solutions to “what is the square root of 4?” — 2 and -2 — there are three equally valid solutions to finding a number’s cube root, four for the fourth power root, etc.
You can easily see why that must be the case in the angular (polar) representation because it’s a consequence of how long it takes the angle parameter to wrap around and repeat.
When n is 3, you get three values, one for k = 0, one for k = 1 and one for k = 2. Thereafter, the values repeat. What looks like an ad hoc aspect of algebra — the relationship between the “root power” and the number of unique root values — is in fact an inevitable consequence of trigonometric values repeating every 2π.
There’s another interesting geometric aspect to roots, too. Because k and n are both integers, their combinations correspond to lines on a graph separated by equal angular values. For cube roots, that angle is 120 degrees (2π/3 radians). You can find the cube root of any two-dimensional (complex) number by drawing lines 120 and 240 degrees away from the line connecting the “traditional” number to the origin of the graph.
For example, to find the cube roots of plain old 1 — or (1, 0) — you could use Euler’s formula with angles of 0, 2π/3 and 4π/3 radians. The lines defined by Euler’s formula are 120 degrees apart, and the roots are:
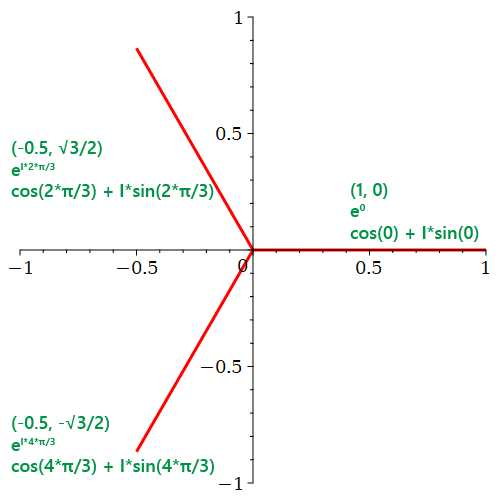
All three representations of the value of each root point are equivalent. They’re just expressed in different forms.
If you raise the upper-left root (-0.5, sin(2π/3)) to the third power you’ll find it evaluates, as expected, to 1. Or at least a close approximation 🙂3:
1.000000001- 3.233738859\times 10^{-10} \mathrm{I}If you’d like to learn more of the unifying concepts between algebra and geometry, read the book :).
But What About Those Tensors?
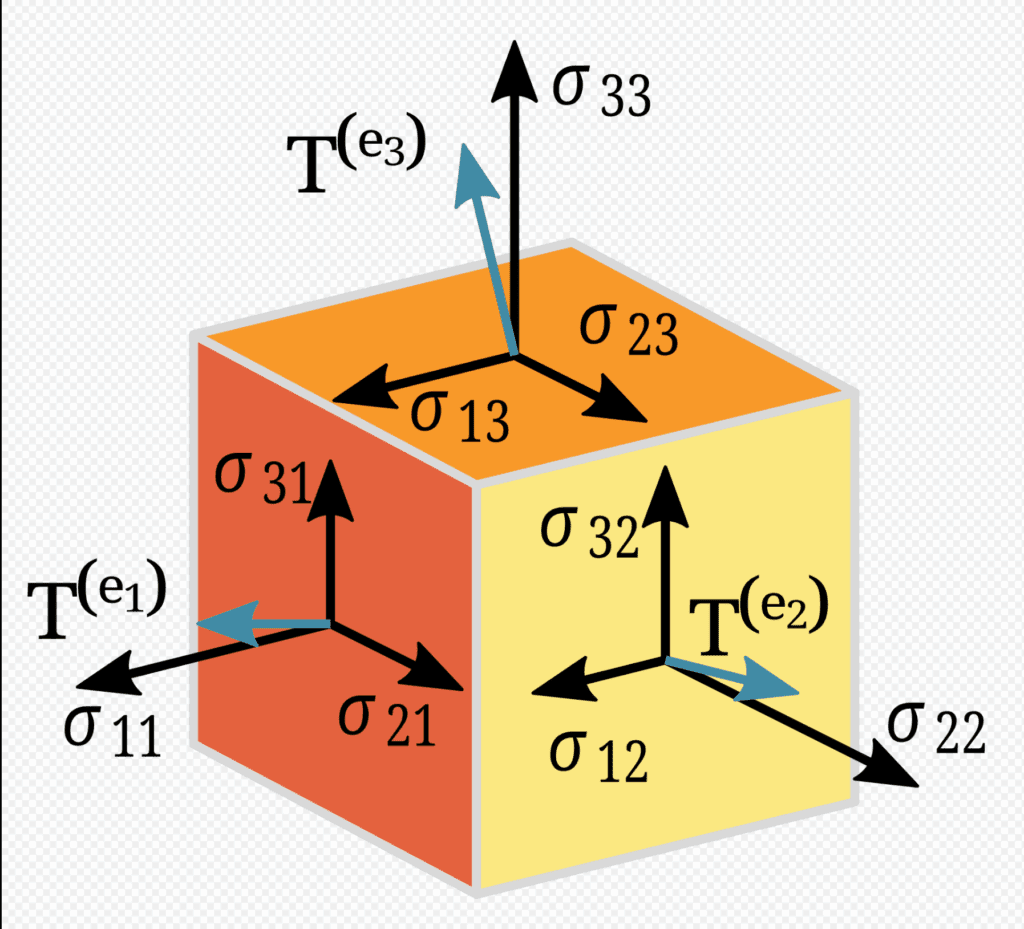
Imagine you want to describe the stress being exerted on an object where the amount and direction of the stress can vary from point to point.
Using the concept of taking your area of interest to smaller and smaller units — taking it to the limit — you’d consider the stresses acting on a “unit cube”, an arbitrary small cube within the object of interest4. You’d have decomposed the stress into a set of perpendicular components, each of which itself would have three components defining the stress in one of the three perpendicular (orthogonal) directions in three-dimensional space. Fully defining the stress would thus require nine numbers for each unit cube/point.
That’s a lot of numbers. Tensors organize those numbers so they can be analyzed collectively, just like vectors organize numbers to define directions.
What’s intriguing — and part of the process of increasing abstraction developed during the 19th and early 20th centuries by mathematicians — is that these abstract collections can, when constrained to follow algebraic rules, represent physical quantities in such a way that the laws of physics (e.g., conservation of linear and angular momentum) fall out of the symbolic analysis. Or so it seems, if I’m understanding Arianrhod correctly5.
As Arianrhod points out multiple times, though, ultimately, when you want to calculate something using those tensor equations, you have to drop down into the individual components. In fact, one of the interesting battles she describes among mathematicians during the 19th century was about what was the point of developing these “useless abstractions” when, in the end, you had to go back to the components to calculate answers anyway. The “abstractionists” won out, eventually, because of the insights afforded by the abstractions…but it consumed a lot of emotional energy, and took many years.
If you enjoy abstract mathematics at all, and are willing to melt your mind a bit, I definitely recommend reading Vectors. If sometimes hard to understand, it’s always insightful…and a joy to read in how it draws connections over centuries of high-powered thought.
To me, that means the designation “imaginary” is just plain wrong. It’d be better to think of it as a required second dimension to what we’d normally take to be a single dimensional value. ↩
Technically, a one-dimensional number can be graphed, too, but why waste time showing its location on a line? You’re not imparting any significant additional information, like you are when more than one dimension is involved. ↩
It doesn’t display exactly as 1 because the sine function generally returns transcendental values. ↩
Differentiating a function in calculus is analogous, except in that case the limit is the “unit length”; any smooth curve can be viewed as an infinite collection of straight line segments. ↩
One of the reasons I plan on re-reading the book and going through all the end notes is to get a better grasp of this, since it seems like a fascinating conclusion in its own right. ↩